Cissoid (from the Gr. κισσός, ivy, and εἰδος, form), a curve invented by the Greek mathematician Diocles about 180 B.C., for the purpose of constructing two mean proportionals between two given lines, and in order to solve the problem of duplicating the cube. It was further investigated by John Wallis, Christiaan Huygens (who determined the length of any arc in 1657), and Pierre de Fermat (who evaluated the area between the curve and its asymptote in 1661). It is constructed in the following manner. Let APB be a semicircle, BT the tangent at B, and APT a line cutting the circle in P and BT at T; take 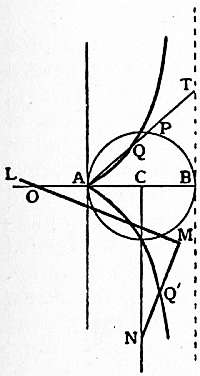a point Q on AT so that AQ always equals PT; then the locus of Q is the cissoid. Sir Isaac Newton devised the following mechanical construction. Take a rod LMN bent at right angles at M, such that MN = AB; let the leg LM always pass through a fixed point O on AB produced such that OA = CA, where C is the middle point of AB, and cause N to travel along the line perpendicular to AB at C; then the midpoint of MN traces the cissoid. The curve is symmetrical about the axis of x, and consists of two infinite branches asymptotic to the line BT and forming a cusp at the origin. The cartesian equation, when A is the origin and AB = 2a, is y²(2a - x) = x³; the polar equation is r = 2a sin θ tan θ. The cissoid is the first positive pedal of the parabola y² + 8ax = 0 for the vertex, and the inverse of the parabola y² = 8ax, the vertex being the centre of inversion, and the semi-latus rectum the constant of inversion. The area between the curve and its asymptote is 3πa², i.e. three times the area of the generating circle.

The term cissoid has been given in modern times to curves generated in similar manner from other figures than the circle, and the form described above is distinguished as the cissoid of Diocles.

A cissoid angle is the angle included between the concave sides of two intersecting curves; the convex sides include the sistroid angle.

---