One possible definition of a fuzzy classifier is given in (Kuncheva 2000) as 'Any classifier that uses fuzzy sets or fuzzy logic in the course of its training or operation'.
Contents |
[edit] Why fuzzy classifiers?
A classifier is an algorithm that assigns a class label to an object, based on the object description. It is also said that the classifier predicts the class label. The object description comes in the form of a vector containing values of the features (attributes) deemed to be relevant for the classification task. Typically, the classifier learns to predict class labels using a training algorithm and a training data set. When a training data set is not available, a classifier can be designed from prior knowledge and expertise. Once trained, the classifier is ready for operation on unseen objects.
Classification belongs to the general area of pattern recognition and machine learning.
- Soft labelling. The standard assumption in pattern recognition is that the classes are mutually exclusive. This may not be the case, as the example in Figure 1 shows. A standard classifier will assign a single crisp label (rain). A fuzzy classifier can assign degrees of membership (soft labels) in all four classes {rain, clouds, wind, sunshine}, accounting for the possibility of winds and cloudy weather throughout the day. A standard classifier can output posterior probabilities, and offer soft labelling too. However, a probability of, say, 0.2 for cloudy weather means that there is 20% chance that tomorrow will be cloudy. A probabilistic model would also assume that the four classes form a full group, i.e., snow, blizzards or thunderstorms must be subsumed by one of the existing four classes. Soft labelling is free from this assumption. A fuzzy classifier, \(D\ ,\) producing soft labels can be perceived as a function approximator \( D:F\to [0,1]^c,\) where \( F\) is the feature space where the object descriptions live, and \(c\) is the number of classes. While tuning such a function approximator outside the classification scenario would be very difficult, fuzzy classifiers may provide a solution that is both intuitive and useful.
- Interpretability. Automatic classification in most challenging applications such as medical diagnosis has been sidelined due to ethical, political or legal reasons, and mostly due to the black box philosophy underpinning classical pattern recognition. Fuzzy classifiers are often designed to be transparent, i.e., steps and logic statements leading to the class prediction are traceable and comprehensible.
- Limited data, available expertise. Examples include predicting and classification of rare diseases, oil depositions, terrorist activities, natural disasters. Fuzzy classifiers can be built using expert opinion, data or both.
[edit] Models of fuzzy classifiers
The broad definition of a fuzzy classifier implies a variety of possible models.
[edit] Fuzzy rule-based classifiers
[edit] Class label as the consequent
The simplest fuzzy rule-based classifier is a fuzzy if-then system, similar to that used in fuzzy control. Consider a 2D example with 3 classes. A fuzzy classifier can be constructed by specifying classification rules, e.g.,
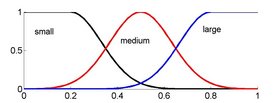
IF \(x_1\) is medium AND \(x_2\) is small THEN class is 1 IF \(x_1\) is medium AND \(x_2\) is large THEN class is 2 IF \(x_1\) is large AND \(x_2\) is small THEN class is 2 IF \(x_1\) is small AND \(x_2\) is large THEN class is 3
The two features \(x_1\) and \(x_2\) are numerical but the rules use linguistic values. If there are \(M\) possible linguistic values for each feature, and \(n\) features in the problem, the number of possible different if-then rules of this conjunction type (AND) is \(M^n\ .\) If the fuzzy classifier comprises of all such rules, then it turns into a simple look-up table. Unlike look-up tables, however, fuzzy classifiers can provide outputs for combinations of linguistic values that are not included as one of the rules. Each linguistic value is represented by a membership function.
\[\tau_1({\mathbf x})=\mu^{(1)}_{medium}(x_1)\;\;\mbox{AND}\;\; \mu^{(2)}_{small}(x_2). \] The superscript \((i)\) is the feature tag. This is needed because the notion of, say, small for \(x_1\) may be different from that for \(x_2\ .\) The AND operation is typically implemented as minimum but any other t-norm may be used. The rule "votes" for the class of the consequent part. The weight of this vote is \(\tau_1({\mathbf x})\ .\)
To find the output of the classifier, the votes of all rules are aggregated. Among the variety of methods that can be applied for this aggregation, consider the maximum aggregation method. The soft class label for \({\mathbf x}\) consists of membership values \(g_k({\mathbf x})\in [0,1]\ ,\) \(k=1,...,c\ ,\) where \(c\) is the number of classes. Let \(i \to k\) denote that rule \(i\) votes for class \(k\ .\) Then \[\tag{1} g_k({\mathbf x}) = \max_{i\to k}\;\tau_{i}({\mathbf x}).\]
The three classes in the example can be thought of as the RGB colours in an image as shown in Figure 3. Class 1 is encoded as red, class 2 as green and class 3 as blue. The dark regions correspond to points in the feature space with very low membership values in all three classes. Labelling of such points may need further analysis. If a crisp label is required, \({\mathbf x}\) is assigned to the class with the largest \(g_k({\mathbf x})\ .\) Figure 4 shows the crisp classification regions.
[edit] Linguistic labels as the consequent
The consequent part of the rule may also contain linguistic values. For example,
IF \(x_1\) is medium AND \(x_2\) is small THEN class 1 is large AND class 2 is small AND class 3 is small.
This type of rule is easier to obtain from a human expert. The classifier in this case operates as a Mamdani-type fuzzy system (Mamdani, 1977). The output is again a soft label containing the values of \(c\) discriminant functions.
[edit] Function as the consequent
This type of fuzzy classifier is based on Takagi-Sugeno fuzzy systems (Takagi and Sugeno, 1985). A generic fuzzy if-then rule for classification is a regressor over the feature data space:
IF \(x_1\) is \(A_1\) and AND \(x_2\) is \(A_2\) AND ... AND \(x_n\) is \(A_n\) THEN \(g_1=\sum_{i=0}^na_{i1}x_i\) AND ... \(g_c=\sum_{i=0}^n{a_{ic}x_i}\ ,\)
where \(A_i\) are linguistic values and \(a_{ij}\) are scalar coefficients (See more details in (Cordon et al., 1999)).
The most useful special case is when the support for each class is a single constant value, usually within the interval [0,1]
IF \(x_1\) is \(A_1\) and AND \(x_2\) is \(A_2\) AND ... AND \(x_n\) is \(A_n\) THEN \(g_1=\beta_1\) AND ... \(g_c=\beta_c\ ,\)
where \(\beta_k\) are constants.
In this model every rule votes for all the classes. The maximum aggregation method will be the same as in equation (1) and the summation will be taken across all the rules. Another popular aggregation method is the weighted sum \[g_k({\mathbf x}) = \frac{\sum_{i}\beta_{k,i}\tau_{i}({\mathbf x})}{\sum_{i}\tau_{i}({\mathbf x})}\ ,\] where \(\beta_{k,i}\) is the consequent constant for class \(k\) in rule \(i\ .\)
[edit] Training fuzzy rule-based classifiers
The critical question is how fuzzy classifiers are trained. Where do the membership functions for the linguistic values come from? How are the rules constructed? How are the consequents determined? There is a myriad of methods for training and fine-tuning among which are fuzzy neural networks (Nauck et al., 1997), genetic algorithms (see Roubos et al., 2003; Ishibuchi et al., 1995), as well as numerous heuristic methods for rule extraction based on the data geometry. Online training of fuzzy classifiers has also been considered (Angelov and Zhou, 2008).
Some fuzzy rule-based classifiers suffer from combinatorial explosion of the number of rules (Kuncheva, 2000). The main reason is that the classifier is trained by partitioning of the data space along each feature (Babuska, 1998). A careful pay-off between accuracy and transparency must be made.
[edit] Fuzzy prototype-based classifiers
There are fuzzy classifier models inspired by the idea of "fuzzifying" conventional classifiers. A typical representative of this group is the K-nearest neighbour classifier (K-nn). In the classical K-nn, the object \({\mathbf x}\) is labelled as the majority of its K nearest neighbours in a reference data set. The approximations of the posterior probabilities for the classes are crude, given by the proportion of neighbours out of k voting for the respective class. Fuzzy K-nn uses the distances to the neighbours as well as their soft labels, if these are available.
The reference set for this classifier does not have to be selected from the existing data. A set of relevant objects (prototypes) with crisp or soft labels can be constructed. The class membership of \({\mathbf x}\) is obtained through combining the similarities between \({\mathbf x}\) and the prototypes. Fuzzy prototype-based classifiers can be related to popular classifier models including Parzen classifier, learning vector quantization (LVQ) and radial basis functions (RBF) neural networks (Kuncheva 2000).
Along with training from data, human expertise can be used. Experts can assign soft labels to prototypes, construct prototypes not present in the training data, specify meaningful types of combination of similarities, etc. Providing this type of expertise is much more intuitive for the domain expert compared to training fuzzy rule-based classifiers. Experts may not be able to explicate the intuitive ways in which they reach a decision about class labels using the jargon of if-then rules and membership functions. On the other hand, in the training of fuzzy prototype-based classifiers the expert insight and intuition do not have to be taken to the fore, analysed and mimicked.
[edit] Fuzzy combination rules for classifier ensembles
In multiple classifier systems (classifier ensembles) the decisions of several classifiers are aggregated to produce a single (crisp or soft) class label. Given an object \({\mathbf x}\ ,\) let \(d_{i,j}({\mathbf x})\in [0,1]\) be the degree of membership that classifier \(i\) suggests for class \(j\ ,\) \(i = 1,...,L\) (number of classifiers), \(j = 1,...,c\) (number of classes). Many conventional classifiers can produce soft labels, usually as estimates the posterior probabilities for the classes, conditioned on \({\mathbf x}\ .\) The matrix \(\{d_{i,j}({\mathbf x})\}\) is called the decision profile for \({\mathbf x}\ .\)
Fuzzy aggregation functions (aggregation rules) abound in fuzzy decision making. The overall support for class \(j\) is calculated using the decision profile entries for that class, which is the \(j\)-th column of the matrix. Given an aggregation function \(A\ ,\) the soft ensemble output for class \(j\) is \[ d_{e,j}({\mathbf x})=A(d_{1,j}({\mathbf x}),d_{2,j}({\mathbf x}),...,d_{L,j}({\mathbf x})).\] Minimum, maximum and mean (order statistics in fuzzy disguise) are the most popular choices for \(A\ .\) Any function \(A:[0,1]^L\to [0,1]\) can be used instead, e.g., product or ordered weighted averaging (OWA) (Yager and Kacprzyk, 1997).
The aggregation can also be made by fuzzy integral, which combines the class support (evidence) with the competence of the classifiers in the ensemble (Kuncheva, 2003).
[edit] References
Kuncheva L.I., Fuzzy Classifier Design, Springer-Verlag, Heidelberg, May 2000.
Mamdani E. H., Application of fuzzy logic to approximate reasoning using linguistic synthesis, IEEE Trans. Computers 26(12), 1977, pp. 1182-1191.
Takagi T. and M. Sugeno, Fuzzy identification of systems and its application to modeling and control, IEEE Trans. on Syst., Man & Cybernetics, 15, 1985, pp. 116-132.
Cordon O., M. J. del Jesus, F. Herrera, A proposal on reasoning methods in fuzzy rule-based classification systems, International Journal of Approximate Reasoning, 20 (1), 1999, pp.22-45, 1999.
Nauck D., F. Klawonn and R. Kruse. Foundations on Neuro-Fuzzy Systems. Wiley, Chichester, 1997.
Roubos J., M. Setnes, J. Abonyi, Learning fuzzy classification rules from data, Information Sciences, 150, 2003, pp.77-93.
Ishibuchi H., K. Nozaki, N. Yamamoto, H. Tanaka, Selecting fuzzy if-then rules for classification problems using genetic algorithms, IEEE Trans. on Fuzzy Systems, 3(3), 1995, pp.260-270.
Babuska R., Fuzzy Modeling for Control, Kluwer Academic Publishers, Boston, USA, 1998.
Angelov P., X. Zhou, Evolving Fuzzy-Rule-based Classifiers from Data Streams, IEEE Transactions on Fuzzy Systems, ISSN 1063-6706, special issue on Evolving Fuzzy Systems, December 2008, vol. 16, No6, pp.1462-1475.
Yager R.R. and J, Kacprzyk (Eds.) The Ordered Weighted Averaging operators. Theory and Applications, Kluwer Academic Publishers, USA, 1997.
Kuncheva L.I. "Fuzzy" vs "Non-fuzzy" in combining classifiers designed by boosting, IEEE Transactions on Fuzzy Systems, 11 (6), 2003, pp. 729-741.
Internal references
- Jan A. Sanders (2006) Averaging. Scholarpedia, 1(11):1760.
- Robert Babuska and Ebrahim Mamdani (2008) Fuzzy control. Scholarpedia, 3(2):2103.
- Lotfi A. Zadeh (2008) Fuzzy logic. Scholarpedia, 3(3):1766.
- Milan Mares (2006) Fuzzy sets. Scholarpedia, 1(10):2031.
- Mirko Navara (2007) Triangular norms and conorms. Scholarpedia, 2(3):2398.
[edit] See Also
Fuzzy c-means cluster analysis, Machine learning, Multiple classifier systems, Pattern recognition