Integration using polar coordinates is a technique for solving integrals using polar coordinates. Sometimes an integral that is complicated in one set or coordinates, such as Cartesian coordinates become very easy or even trivial in polar coordinates.
Example[edit]
Consider the integral
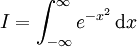
This can be converted into polar coordinated by multiplying 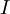 by itself, so that
by itself, so that

This can be expressed as the double integral,
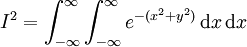
Now the usefulness of polar coordinates becomes apparent as in polar coordinates, 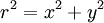 . The bounds mean the integral is over the entire x-y plane, so
. The bounds mean the integral is over the entire x-y plane, so 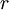 varies from
varies from 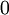 to
to 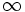 and
and 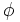 from
from 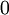 to
to 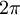 . To convert the differentials, we must multiply by the Jacobian,
. To convert the differentials, we must multiply by the Jacobian, 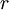 to get
to get
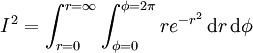
This can be integrated by separating the integral. The 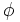 integral gives
integral gives 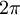 and the
and the 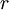 integral gives
integral gives 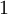 . This means the initial integral,
. This means the initial integral, 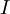 is
is 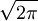 .
.
Other methods of integration[edit]
The primary methods of integration include:
- Integration by parts
- Integration using polar coordinates
- Multiple integration
- Residue calculus (for definite integrals)
- Method of simultaneous convolutions
- Mellin transforms
- Inflation-restriction sequences